이번 글에서는 컴퓨터에서 오디오 데이터를 처리하기 위해
우리가 듣는 소리를 디지털 바이너리 데이터로 추출/변환하여 처리하는 방법을 다룬다.
▼단, 아래의 소리 기초 원리에 대한 이해가 필요하다.▼
소리란? 소리의 기초 원리 (feat. 마이크와 스피커의 작동 원리)
소리의 진폭, 주기, 주파수, 파형 (볼륨, 음정, 음색의 결정 원리)
# 컴퓨터가 소리를 다루는 원리
컴퓨터가 소리를 인식하고, 소리를 재생하는 원리는 무엇일까?
1. 소리가 발생하면 주변의 공기가 진동하여 마이크의 판막을 흔든다.
2. 마이크의 판막이 진동할 때마다 전기 신호가 생성된다.
3. 전기 신호가 메모리에 디지털 데이터(1, 0)로 저장된다.
(ADC: Analog to Digital Conversion)
4. 저장된 데이터가 CPU에 의해 적절히 연산처리 된다.
5. 연산처리된 데이터를 이용해 스피커에 전기신호를 송출한다.
(DAC: Digital to Analog Conversion)
6. 스피커는 전기 신호에 따라 적절히 판막을 진동시킨다.
* 앰프를 이용하면 소리를 크게 진폭시킬 수 있다.
7. 스피커가 발생시킨 공기의 진동이 우리의 귀에 들어와 고막을 흔든다.
8. 우리의 뇌는 고막의 흔들림을 해석하여 아름다운 음악 소리로 느끼게 해준다.
아래의 그림은 이런 일련의 흐름을 보여준다.

# ADC(Anlaog to Digital Conversion)
소리는 공기의 밀도 변화가 연속되는 지극히 아날로그적인 현상이다.
이러한 연속 신호를 컴퓨터에서 다루기 위해서는 0101 형태의 바이너리 데이터로 변환해야만 한다.
그리고 mp3 같은 디지털 형태로 저장된 음원을 귀로 듣기 위해서는
0101로 이루어진 파일을 다시 아날로그로 변환하여 전기 신호를 내보내고
스피커나 이어폰을 통해 공기의 진동을 만들어 소리를 재현해야 한다.
정리하면,
ADC(Analog to Digital Conversion)란
아날로그 형태의 연속 신호인 소리를 디지털 형태의 바이너리 데이터로 변환하는 것이다.
DAC(Digital To Analogu Conversion)란
디지털 형태의 바이너리 데이터를 다시 아날로그 형태의 연속 신호인 소리로 변환하는 것이다.

즉, ADC와 DAC는
소리라는 연속적인 공기의 밀도 변화(Analog)를 이산적인 데이터(Digital)로 전환하고 역전환하는 것을 의미한다.
# 오디오 샘플링(Sampling)에 대하여
"연속" 신호는 "무한대"의 값을 갖는다.
따라서 연속 신호 전체를 분석하는 것은 불가능하며, 일부 데이터만 추출해서 사용해야 한다.
1. 샘플링(Sampling)
연속적인 오디오 신호에서 일부를 추출하는 것을 샘플링(Sampling)이라고 한다.
특정 시점의 진폭값들을 추출하여 이산 디지털 데이터 형태로 저장한다.

2. 샘플(Sample)
샘플링하여 추출한 데이터를 샘플(Sample)이라고 한다.

3. 샘플링 레이트(Sampling Rate)
1초 동안 샘플링한 횟수를 샘플링 레이트(Sampling Rate)라고 한다.
단위는 Hz를 쓰며, 44,100 Hz(44.1 kHz)면 1초에 44,100 개의 샘플을 추출한 것이다.
*주파수와 샘플레이트의 단위가 Hz로 같지만, 측정하는 것은 엄연히 다르다.
* 주파수는 1초 동안 소리의 주기가 반복되는 횟수이고, 샘플레이트는 1초 동안 추출한 오디오 데이터 갯수를 의미한다.
샘플 레이트가 높으면 더 촘촘하게 데이터를 추출하므로 더 정확히 분석할 수 있지만, 효율성 및 연산 속도가 떨어질 수 있다.
그렇다고 샘플링 레이트가 너무 낮으면 효율성 및 속도는 올라 가겠지만, 원본 데이터를 제대로 분석할 수 없게 된다.
(샘플링 레이트가 높으면 손실이 적다고 표현하기도 한다.)
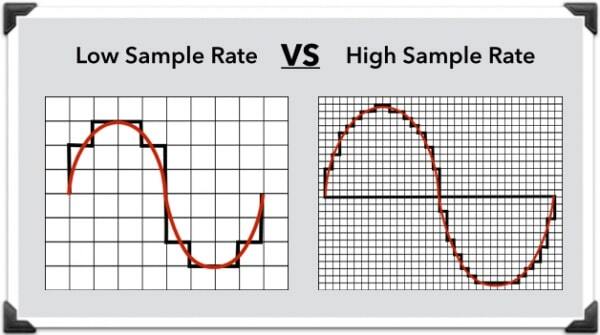
그래서 적절한 샘플레이트로 샘플링하는 것이 중요한데,
여기서 나오는 것이 Nyquist Theorem 이다.
4. 나이퀴스트 정리(Nyquist Theorem)
나이퀴스트 정리는
특정 주파수 대역(Hz)의 소리를 분석하려면, 샘플링 레이트(Hz)가 최소 2배 이상 되도록 샘플링 해야 한다는 것이다.
역으로 말하면, 샘플링 레이트(Hz)의 절반에 해당하는 주파수 대역(Hz)의 소리만 분석 가능하다는 것이다.
이게 당췌 무슨 말일까?
예를 들어 1초동안 [위-아래]의 주기를 2번 반복하는 2 Hz 주파수의 파형이 있다고 하자.
아래와 같은 [위-아래-위-아래]의 파형을 갖게 될 것이다.
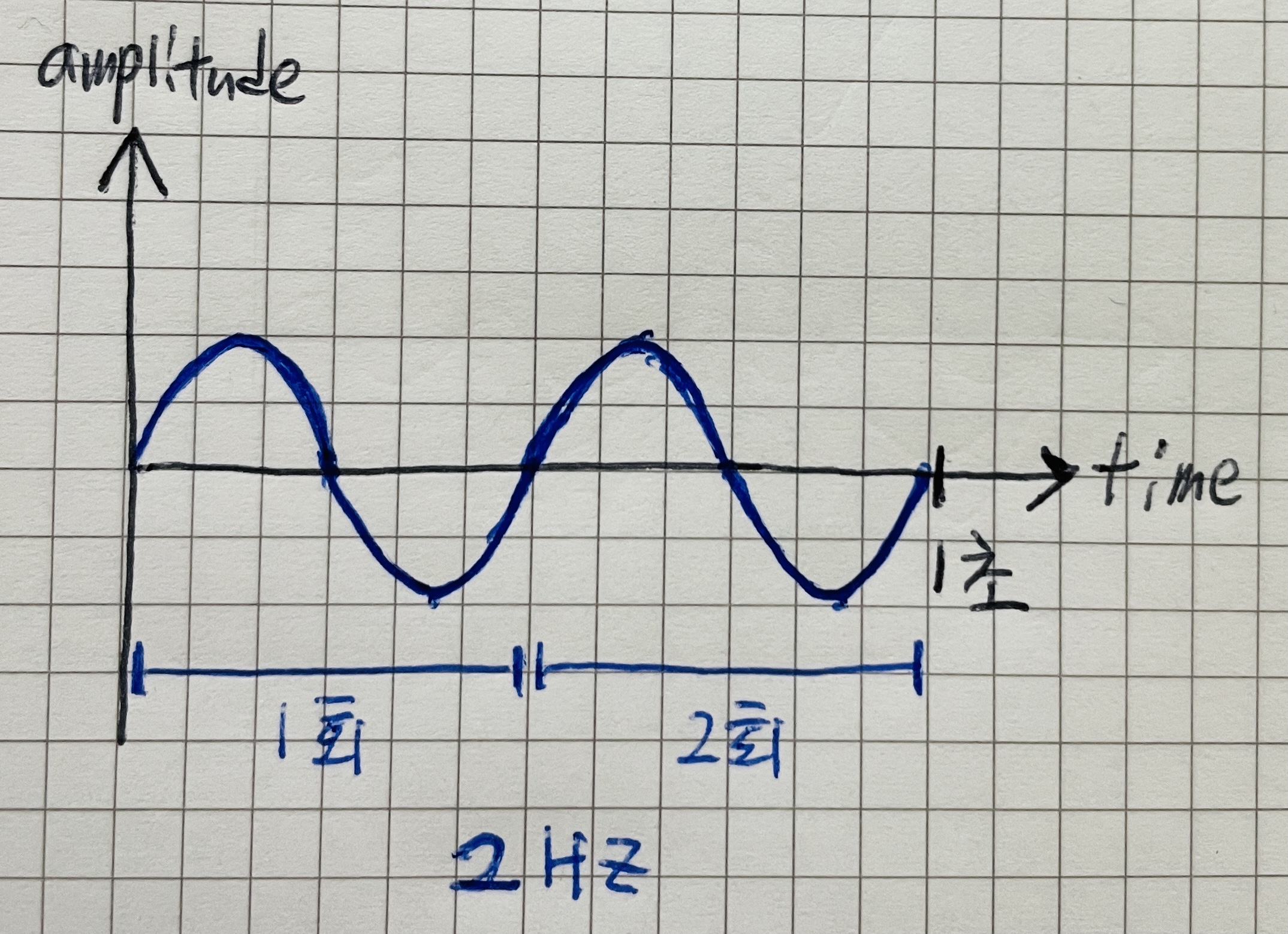
이 경우, 샘플링을 몇번 해야할까?
주파수가 2 Hz니까, 샘플링레이트도 2Hz로 샘플링해보자.

이렇게 되면 추출한 샘플들이 원본 아날로그 소리를 대표하지 못하게 된다.
최소한 1초에 4회 정도는 샘플링을 해야 [위-아래-위-아래]의 파형을 파악할 수 있을 것이다.
(즉, 샘플레이트가 4 Hz는 되어야 한다)
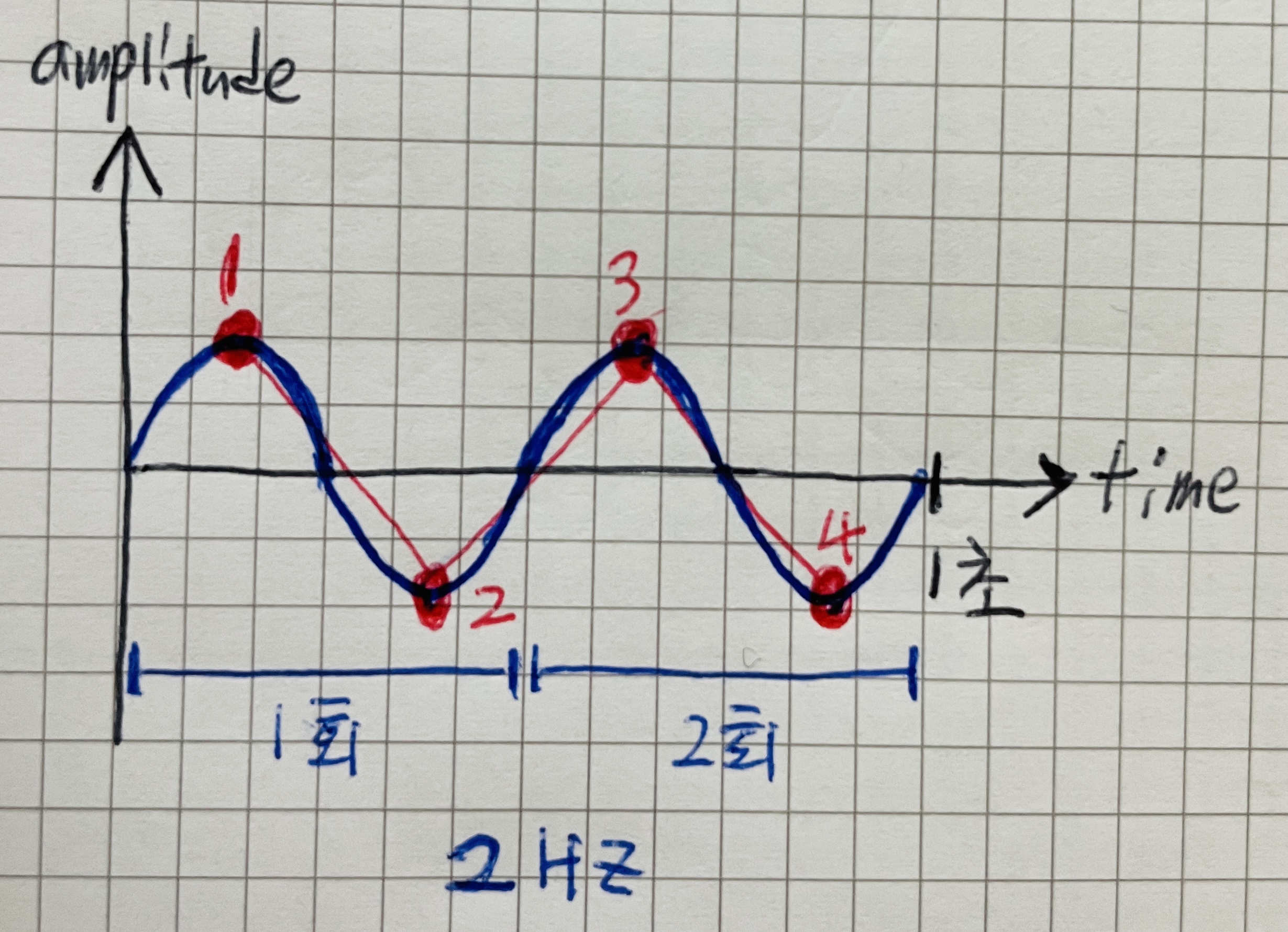
그래서 샘플링 레이트가 분석하려는 주파수 대역의 최소 2배 이상은 되어야
원본 아날로그소리를 대표할 수 있다는 것이 나이퀴스트 정리의 의미다.
다시 한번 정리하면,
나이퀴스트 정리는
샘플링 레이트는 분석하려는 주파수의 2배가 되어야 하고,
샘플링 레이트의 절반에 해당하는 주파수 대역의 소리만 분석 가능하다는 것이다.
예를 들면
샘플링 레이트가 44.1 kHz(44,100 Hz)라면
주파수 대역이 0~22,050 Hz 사이인 소리만 분석 할 수 있다는 것이고,
주파수 대역이 0~22,050 Hz 인 소리를 분석하려면
샘플링 레이트가 44.1 kHz(44,100 Hz)는 되어야 한다는 것이다.
5. 가청 주파수
일반적으로 샘플링 레이트는 44.1 kHz(44,100 Hz)를 기본으로 사용한다.
나이퀴스트 정리를 적용하면 그 이유를 알 수 있다.
1초에 44,100 번 샘플을 뽑는 경우,
1초에 22,050 번 이내로 주기가 반복되는 소리만 분석 가능하다.
(샘플링 레이트 44,100 Hz => 분석 가능 주파수 22,050 Hz)
왜 주파수 20,000 Hz 이내의 소리만 분석할까?
인간이 들을 수 있는 가청 주파수 대역이 20Hz~20,000 Hz 이기 때문이다.
따라서 20,000 Hz를 넘어가는 고주파수의 소리는 분석할 필요가 없기 때문에
기본 샘플링 레이트를 44.1 kHz(44,100 Hz)로 사용하는 것이다.
이런 이유로
CD나 mp3 파일의 샘플레이트도 44.1 kHz 를 사용했던 것이다.
6. 채널(Channel)
오디오 채널이란 녹음/재생하는 신호의 수를 의미한다.
마이크 1개로 녹음하고, 스피커에서 1개에서 재생하면 1채널이다.(=모노)
L, R 의 구분이 없기 때문에 여러개의 스피커로 재생해도 하나의 소리가 똑같이 재생된다.
마이크 2개로 녹음하고, 스피커 2개를 통해 서로 다른 소리를 각각 재생하면 2채널이다.(=스테레오)
2개의 마이크로 녹음하기 때문에 L, R의 녹음본이 다르다.
따라서 2개의 스피커로 재생하면, 각각 다른 녹음본이 재생되어 공간감이 생긴다.
채널의 갯수에 따라 모노, 스테레오 등의 이름을 붙여 부르는데 아래의 도표와 같다.

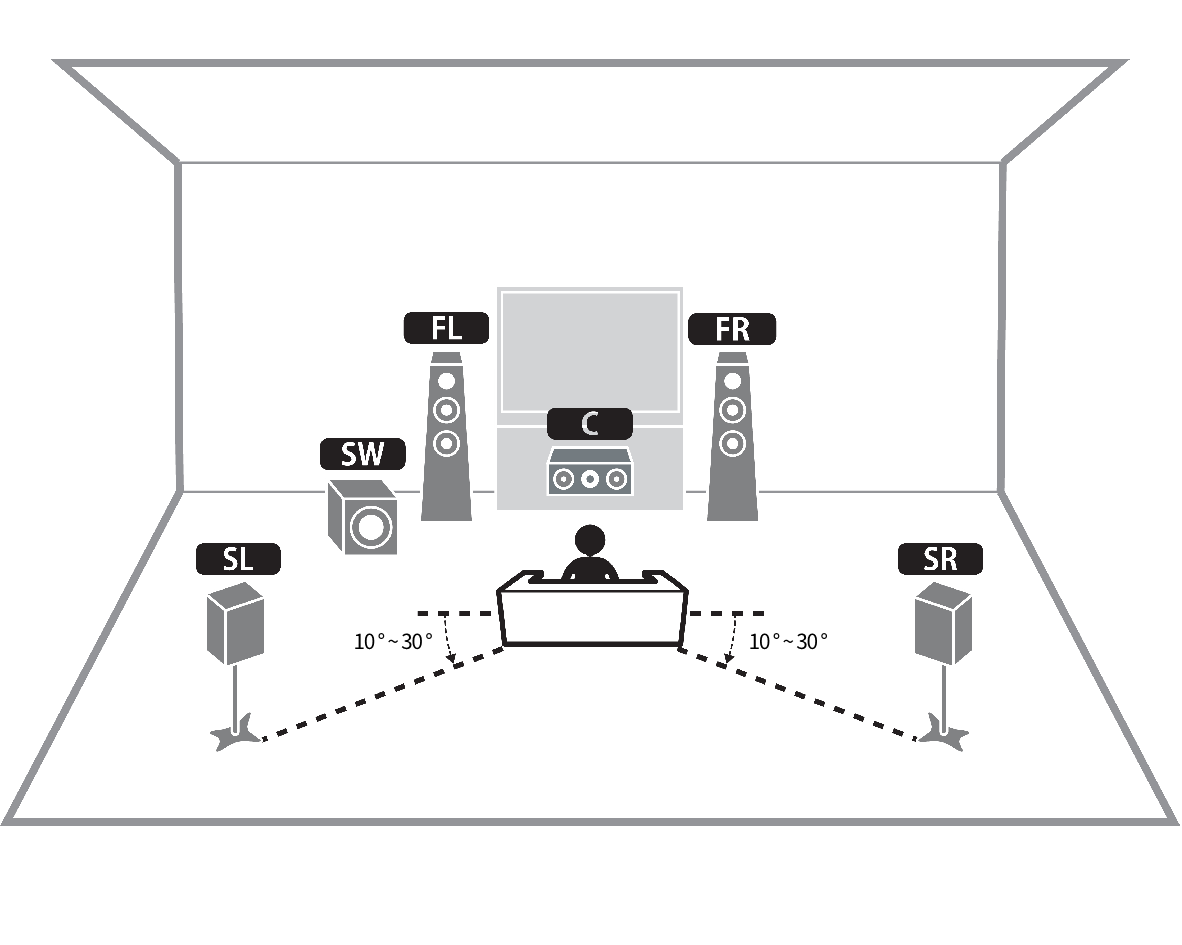
우퍼는 0.1로 친다.
그래서 아래와 같이 SubWoofer를 포함한 5.1채널 서라운드 사운드 구성도 가능하다.
7. 샘플 프레임(Sample Frame)
샘플 프레임은 특정 시점에 추출한 채널별 샘플들의 집합이다.
예를 들어 2채널의 경우,
마이크 2개로 녹음한 소리에서 샘플링을 하면 L측 샘플과 R측 샘플이 각각 추출된다.
샘플 프레임은 L측 샘플과 R책 샘플을 포함하는 단위라고 보면 된다.

만약 2채널 오디오를 44.1 kHz(44,100 Hz)의 샘플링 레이트로 샘플링한다면
44,100개씩 2채널이므로 총 88,100 개의 샘플이 수집되고,
샘플 프레임은 44,100개가 된다.
(샘플 프레임 1개 = L샘플 1개 + R샘플 1개)
즉, 하나의 샘플 프레임은 채널 수 만큼의 샘플로 구성된다.
반대로 생각하면
1채널(모노)의 경우 44.1 kHz의 샘플프레임을 재생하면 1초동안 44,100개의 샘플이 재생된다.
2채널(스테레오)의 경우엔 1초동안 88,200개(L: 44,100개 + R: 44,100개)의 샘플이 재생된다.
그러나 둘다 재생된 샘플 프레임의 갯수는 44,100개로 동일하다.
따라서 아래와 같은 정리가 가능하다.
샘플프레임 갯수 = 샘플링레이트
샘플프레임 갯수 x 채널 = 샘플 갯수
이번 글에서는 오디오 데이터 분석을 위해
연속 신호인 소리에서 이산 디지털 데이터를 추출/변환하는 과정인 ADC 및 샘플링에 대해 다루었다.
이제 본격적으로 소리에 대한 분석이 시작된다.
▼다음 글에서는 추출한 오디오 데이터를 실제로 분석하는 방법을 다룬다.▼
오디오 파형 분석(FFT: 고속 푸리에 변환): Time Domain Data to Frequency Data
'개발(Development) > Media(오디오&비디오 개발)' 카테고리의 다른 글
| 자바스크립트 Media Capture and Streams API: MediaStream, MediaStreamTrack (0) | 2021.12.03 |
|---|---|
| 스트리밍(Streaming)이란: 스트림(Stream), 버퍼(Buffer) 원리 (0) | 2021.11.27 |
| 오디오 파형 분석(FFT: 고속 푸리에 변환): Time Domain Data to Frequency Data (0) | 2021.11.26 |
| 소리의 진폭, 주기, 주파수, 파형 (볼륨, 음정, 음색의 결정 원리) (0) | 2021.11.24 |
| 소리란? 소리의 기초 원리 (feat. 마이크와 스피커의 작동 원리) (0) | 2021.11.22 |




댓글